Turing and the Halting Problem

It was once a dream of Gottfried Leibniz to be able to craft a successful machine that could deduce whether some mathematical statement is true or not. Unfortunately, this dream in the 1700s was not realised, and we must fast forward to 1920s to see the issue resurface by the name of David Hilbert’s “Entscheidungsproblem”, German for “decision problem”. In this case, Hilbert questioned that when given some conditions, is there an algorithm that can always give a “Yes” or “No” determining if the mathematical statement is universally valid. Hilbert was adamant at this time that there is no such thing as an unsolvable problem.

Both Alonzo Church and Alan Turing showed in 1935-36 that this was in fact not true, and the Entscheidungsproblem is, in fact, unsolvable. There is no way to show that a mathematical statement can be evaluated with certainty, let alone prove whether there is a way to show this is true or even false.

This is very similar to the Halting Problem, which the Church-Turing thesis also proved was undecidable. If given an algorithm A and some input data D, is there an algorithm H that decides whether or not the algorithm with that data input will halt or not. It doesn’t matter whether it does halt or not, since it was not possible to even determine whether we can find this out, since no such algorithm exists. The Halting Problem is an example of the Entscheidungsproblem, since the latter questions whether such an algorithm exists and evaluates any possible mathematical statement satisfying some mathematical base rules.

This discovery had great significance because Alan Turing showed that this is the case with Turing machines, the first theoretical development of a machine that could compute a given algorithm following basic instructions. Similarly, Church proved a year earlier how the Entscheidungsproblem was not decidable by way of lambda-calculus, which Turing found was equivalent to the Turing machine.

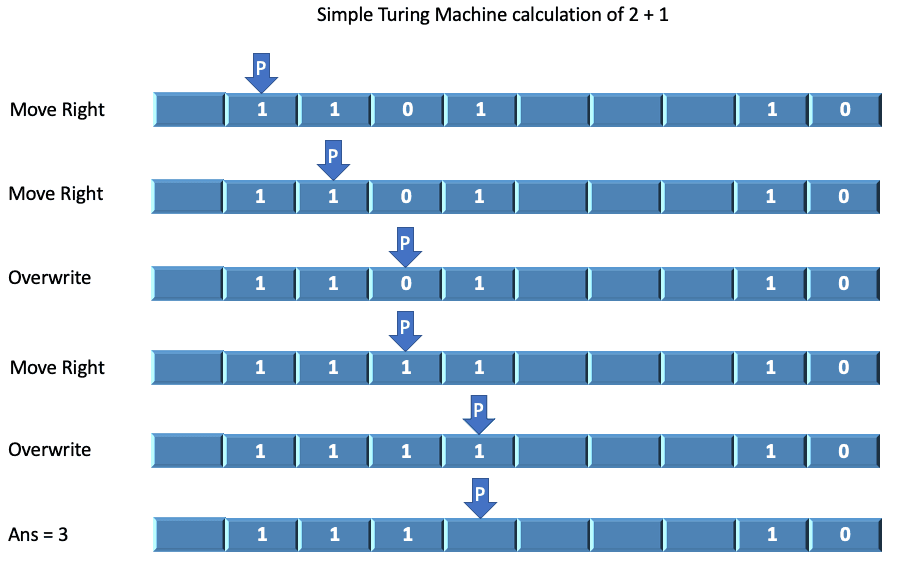
A Turing Machine is a theoretical machine that consists of a strip of tape with a bunch of either empty block spaces, 1s or 0s. There is a pointer which points to the current tape block, and you can only do three operations – either you could move the tape one click to the left, one click to the right, or overwrite the current block which the pointer was pointing to.

Let’s apply a reductio ad absurdum proof, which can be considered as a reduction to absurdity or proof by contradiction. Turing applied the Halting Problem issue to the context of whether a Turing Machine can determine if a Turing machine halt or not, known as the universal Turing machine. We list the possible Turing machines labelled Ti, and for each set of input data D, we find out whether or not it halts. We can write 1 if it does halt, and 0 if it doesn’t halt, thereby we have a full comprehensive binary number for each row.

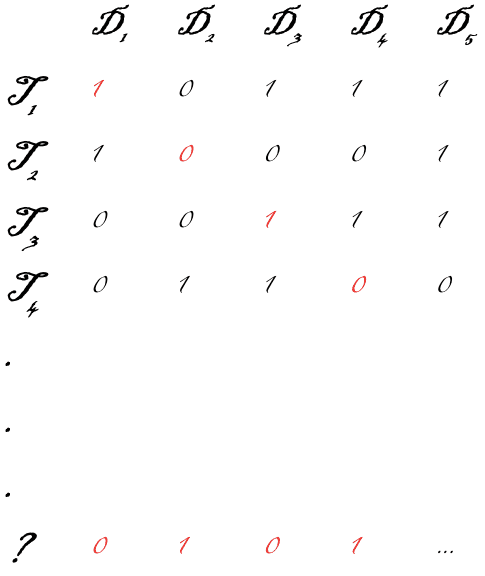
If we take all the diagonal elements from the table, so the 1st element from row 1, 2nd element from row 2, and flip them so if they’re a 1, we write 0 and vice versa, we’ll end up with a binary number. Now since this is not the same as the 1st row, since the 1st digit is not the same, this is not the same as the 2nd row since the 2nd digit is not the same, and so on, we realise this binary number is actually unique, and was never in the list. This means we didn’t account for some Turing machine with all the same data inputs which can be encoded with this binary number, so the list of all Turing machines is not comprehensive, i.e., not countable! We thought we included all the possible Turing machines, but since we can’t even list them all, we cannot find a Turing machine that will determine whether a Turing machine will halt or not, hence undecidable or unsolvable.

This style of layout is called Cantor’s diagonalization, a proof to show that something cannot be countable and is a common technique that falls under discrete mathematics. The proof was in the context of the Halting problem, but Turing found that this problem reduced to the Entscheidungsproblem anyway!

Turing machines, along with lambda-calculus by Church would pave the way for many other formalisations of concepts in computer science that would shape how algorithms and programming languages function today, which is why these were so significant in the history of modern Computer Science. Most programming languages today are Turing-complete, meaning they can be emulated by a Turing machine, which also means that they too are undecided by the Halting Problem!

There are some languages which are not Turing complete (like JSON and HTML), and therefore can always be solved, but the Halting Problem and Entscheidungsproblem focused on a universal halting checker for any statement given some very primitive base rules. Recursion and iteration are not possible in these non-Turing-complete languages but are the bedrock of most imperative programming languages (like Python and Java), whereas Church’s work on lambda calculus is the foundation of most functional programming languages today (Like Haskell).